III.
Résolution numérique de l’équation de LangevinPour pouvoir faire une simulation numérique, il nous faut discrétiser le temps. Le temps le plus court du problème est le temps de corrélation t *, nous le choisissons comme pas. Ce qui donne l’équation itérative suivante :
![]()
![]()
Pour chaque valeur de t, la force F(t) est un nombre aléatoire tiré sur l’intervalle [-Fmax,Fmax].
On choisit ![]() pour que la variance soit
pour que la variance soit ![]() .
.
2) Réalisation d’une force aléatoire
:On choisit D=1, t *=1 et t =20.
Réalisation de la force aléatoire et évolution de la vitesse en fonction du temps et de la vitesse initiale, pour v(0)<< t :
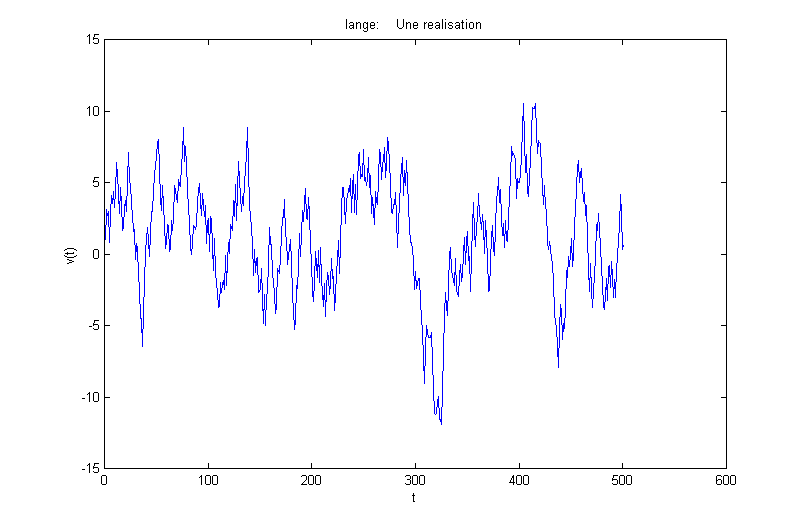
Réalisation de la force aléatoire et évolution de la vitesse en fonction du temps et de la vitesse initiale, pour![]() :
:
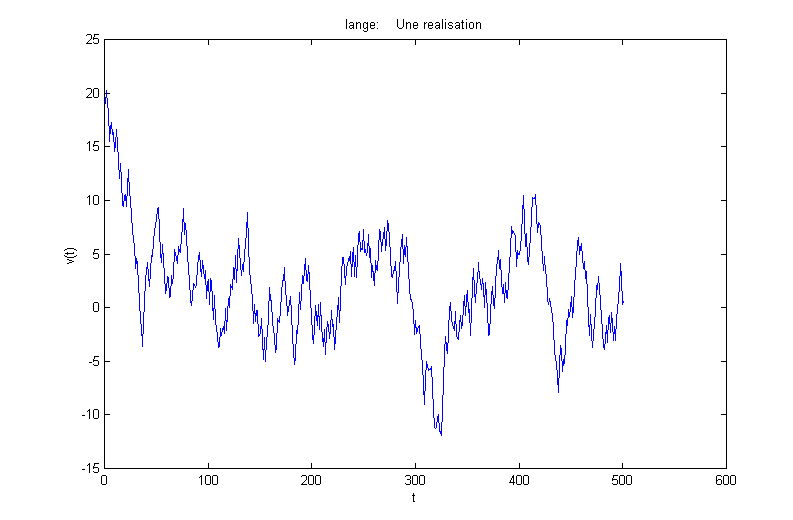
Réalisation de la force aléatoire et évolution de la vitesse en fonction du temps et de la vitesse initiale, pour v(0)>>t :
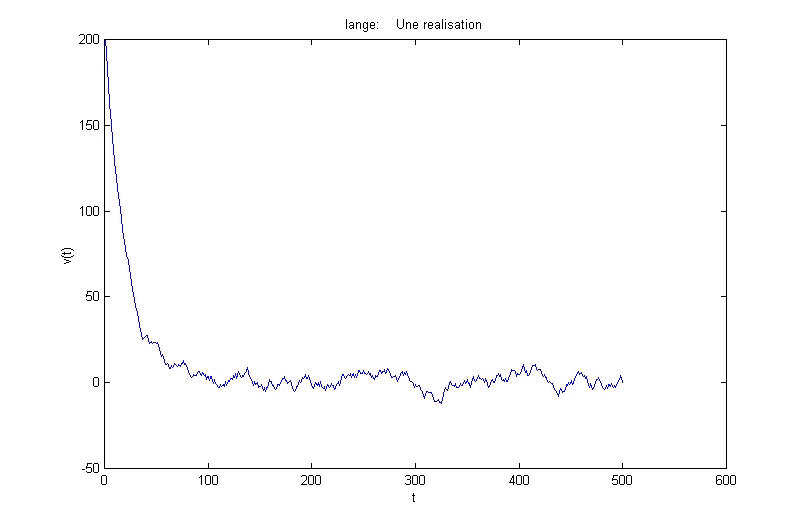
On suppose qu’à l’instant t=0, la vitesse de la particule a une valeur bien définie : v0. Il n’y a pas de force extérieure appliquée. La solution de l’équation de Langevin pour cette condition initiale s’écrit :![]()
![]()
La vitesse de la particule est une fonction aléatoire du temps. Comme en moyenne la force fluctuante est nulle, il vient :
![]()
La vitesse moyenne s’amortit donc, avec le temps de relaxation t . Ce qui est parfaitement illustré par les graphiques précédents.
Nous résolvons l’équation de Langevin pour plusieurs réalisations (R) de la force aléatoire. La moyenne d’ensemble sur les réalisations s’écrit :
![]()
vj(t) est la solution pour la jème réalisation.
On obtient les résultats suivants pour la moyenne et la variance (en fonction de la vitesse initiale vj(0)=0) :
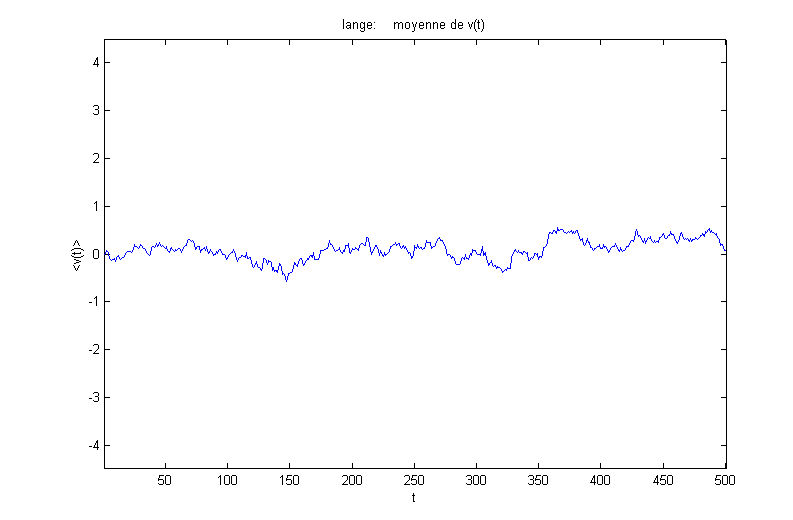
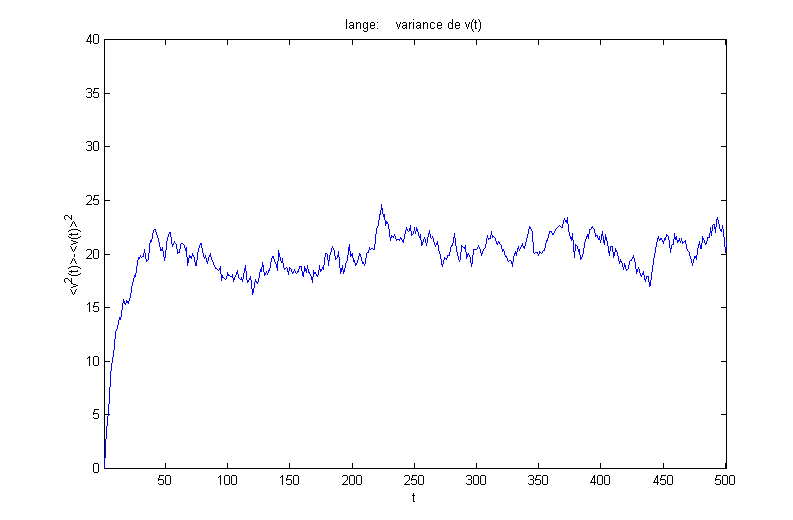
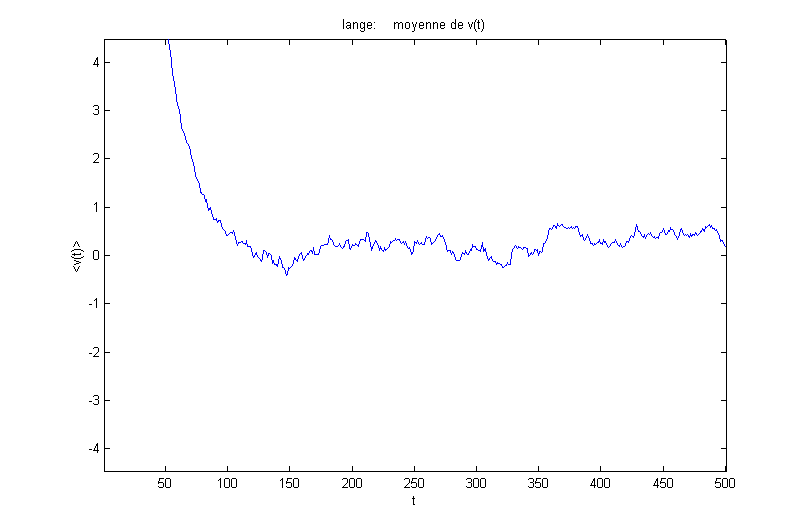
On obtient les résultats suivants pour la moyenne et la variance (en fonction de la vitesse initiale vj(0)=3t
) :
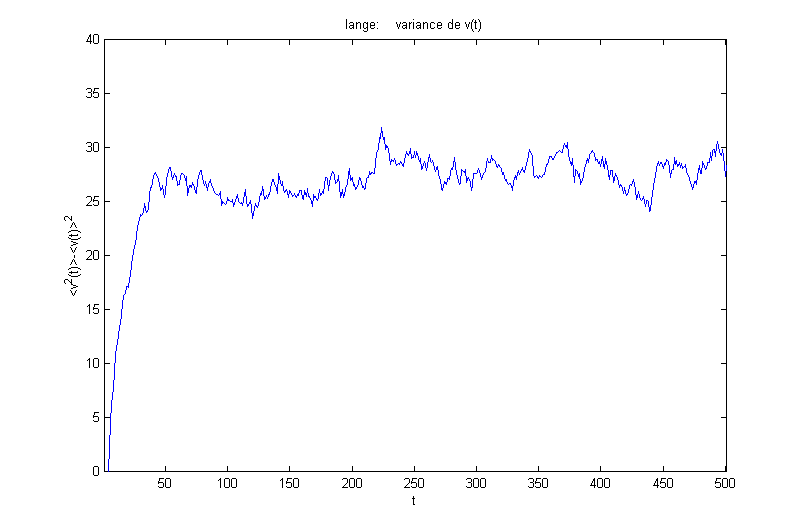
On obtient les résultats suivants pour la moyenne et la variance (en fonction de la vitesse initiale![]() ) :
) :
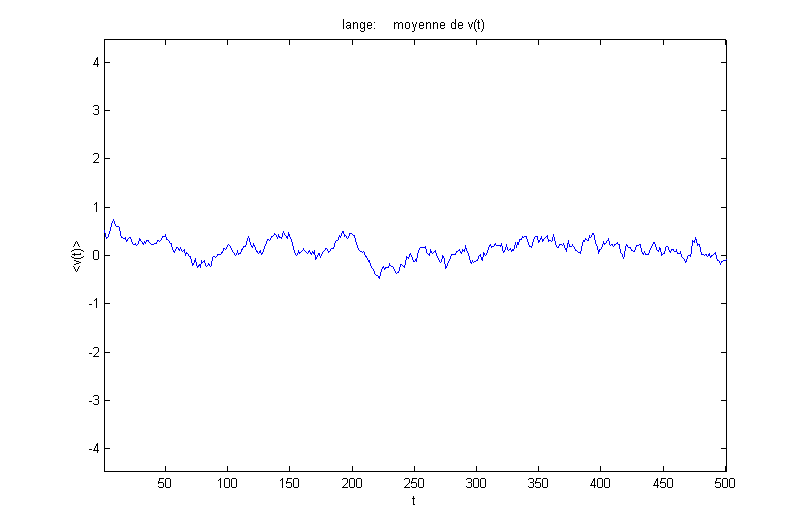
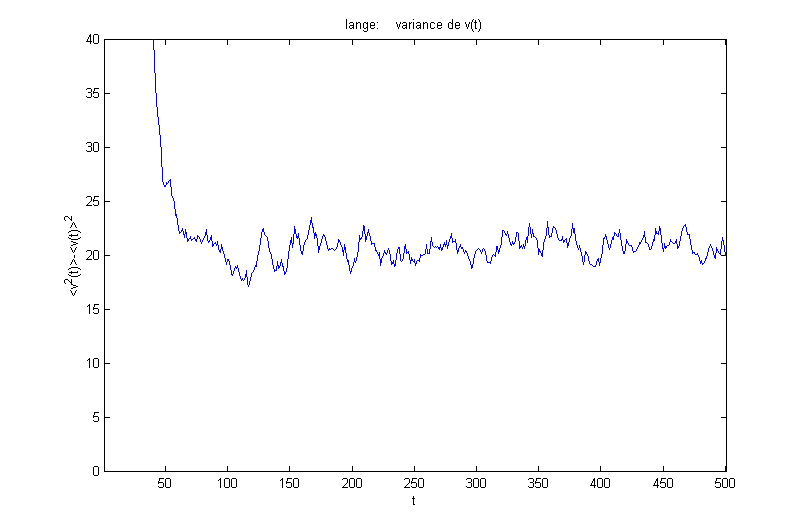
La variance de la vitesse est définie par :
![]()
En remplaçant v(t) par son expression écrite précédemment il vient :
![]()
En prenant la fonction d’autocorrélation de la force de Langevin on obtient :
![]()
soit
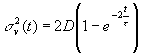
A l’instant t=0, la variance de la vitesse est nulle, et la vitesse est en effet certaine. Sous l’effet de la force aléatoire, des fluctuations de vitesse apparaissent. La variance de la vitesse augmente avec le temps. Pour t<<t , cette croissance est linéaire :
![]()
Il s’agit d’un phénomène de diffusion dans l’espace des vitesses. D est le coefficient de diffusion dans l’espace des vitesses. Pour t>>t , la variance sature à la valeur t D.
On peut tracer pour quelques valeurs représentatives du temps, la distribution P[v(t)] :
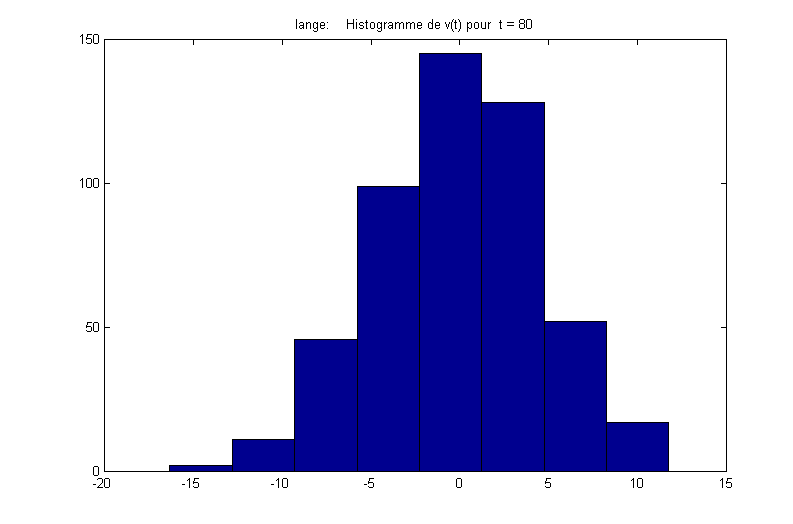
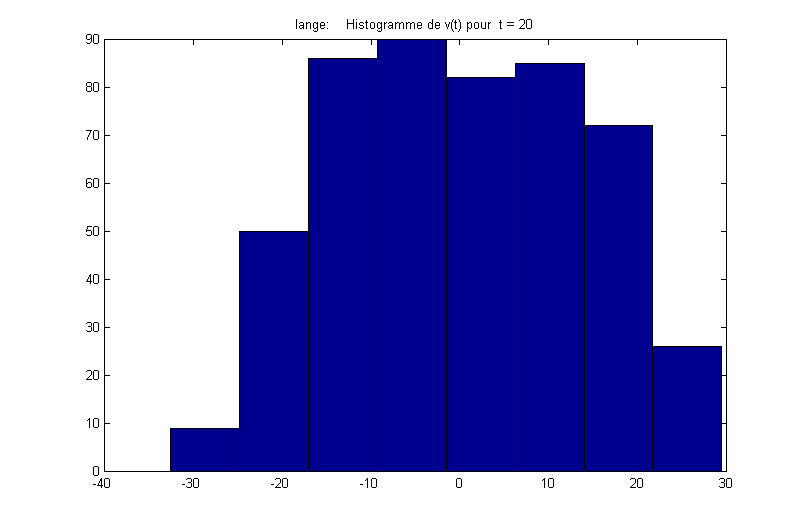
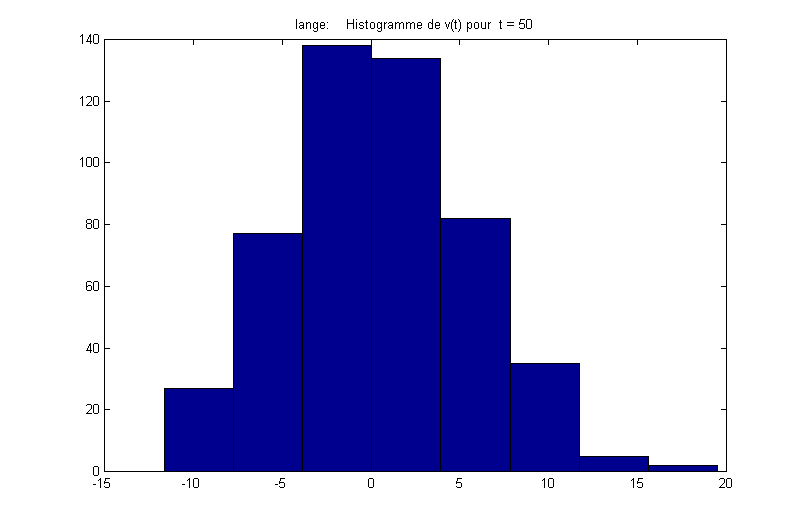
On calcule numériquement, dans le régime d’équilibre, la fonction de corrélation :
![]()
Théoriquement, pour obtenir l'évolution de la vitesse v(t) lorsque la particule brownienne est à l'équilibre, on commence par écrire la solution de l'équation de Langevin pour une fluctuation initiale de vitesse donnée. Pour une fluctuation v0 ayant lieu à l'instant t0, la vitesse à l'instant t s'écrit :
![]()
Si l'instant t0 est reporté à -¥ , la particule brownienne est, à l'instant t, en équilibre avec le bain, et sa vitesse est :
![]()
La valeur de la fluctuation initiale de vitesse est alors "oubliée" : la vitesse de la particule brownienne à l'équilibre à l'équilibre est processus aléatoire stationnaire. On peut donc écrire (t³ t') :
![]()
Si, en première approximation, on néglige le temps de corrélation de la force de Langevin, il vient, en tenant compte de l'expression de la fonction de corrélation entre la force de Langevin et la vitesse :
![]()
Soit, en posant s = t-t' :
![]()
Les simulations numériques donnent les résultats suivants :
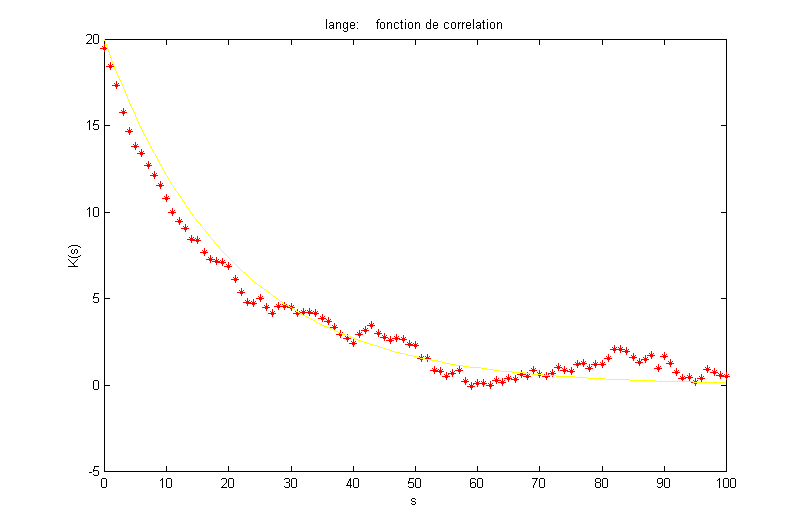
Les courbes théorique (trait plein) et numérique (étoile) se correspondent bien.
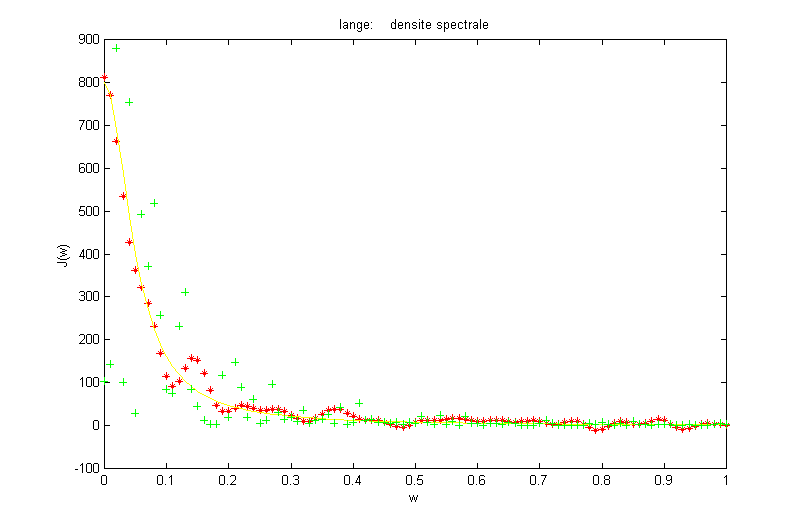
5) Densité spectrale :
On a :
![]()
En utilisant la relation de Wiener-Khintchine, il vient :
![]()
La densité spectrale théorique est une lorentzienne :
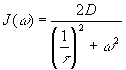
On peut aussi calculer la densité spectrale par :
![]() avec
avec ![]()
Si on compare les courbes théorique et numérique ce quelle que soit la méthode, on voit qu'elles sont très proches.
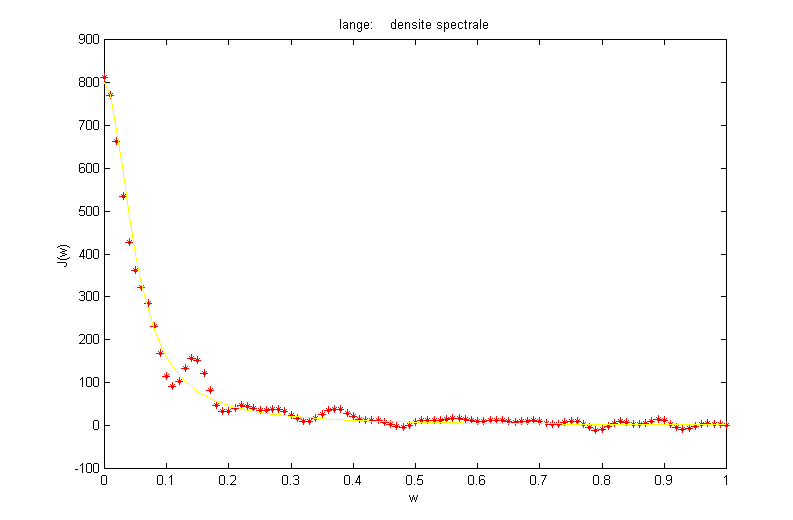
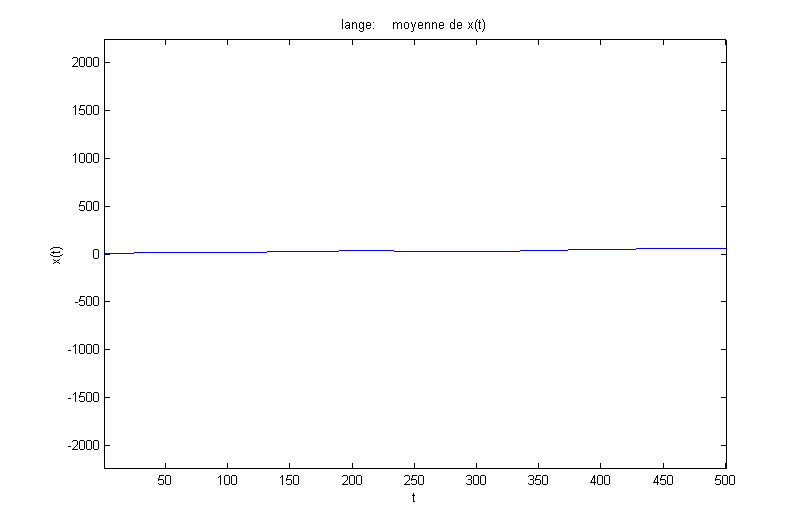
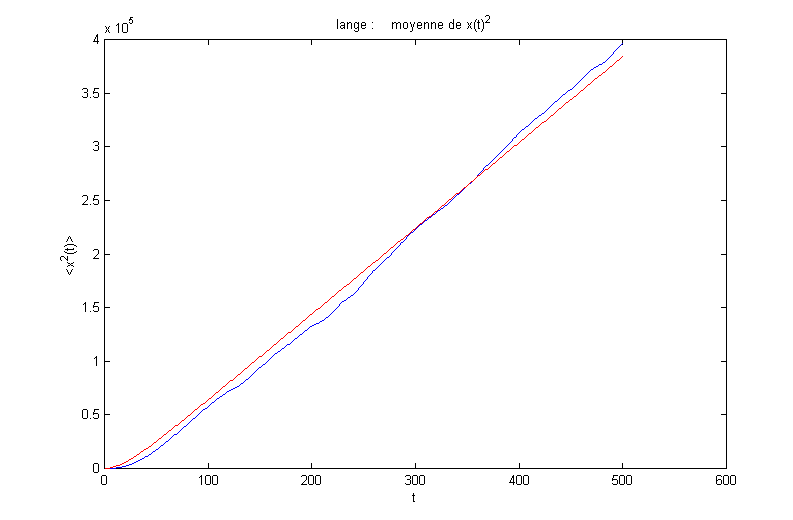
6) Moyennes pour la position :
En utilisant le fait que :
![]()
Les résultats théoriques donnent :
![]() et
et ![]()
On obtient les résultats suivants :
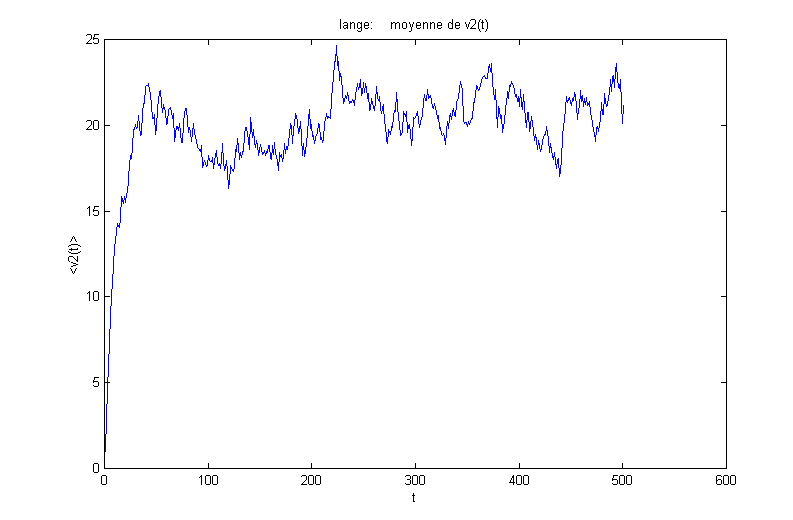
7) Hypothèse ergodique :
On vérifie l'hypothèse ergodique. En effet, que se soit sur un grand nombre de réalisations ou un temps long, on retrouve les même résultats.
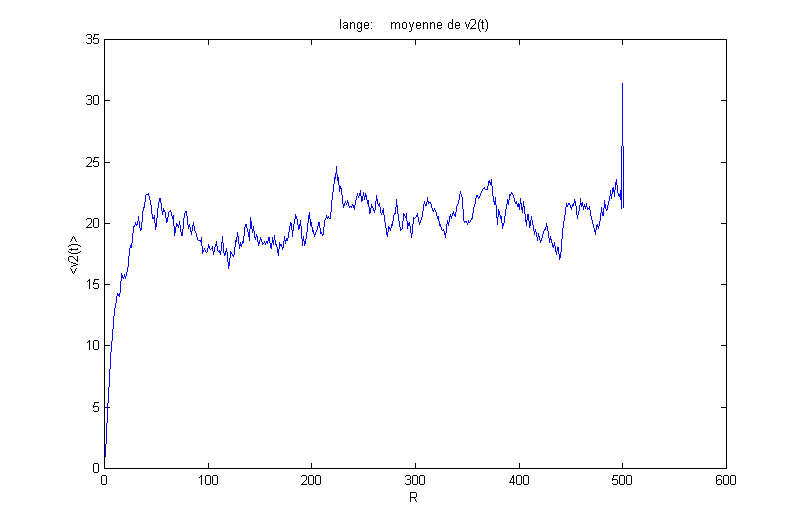
8) Autre force de frottement :
Prenons une force de frottement de la forme :
![]()
L’équation itérative s’écrit alors :
![]()
![]()
On obtient alors les résultats suivants :
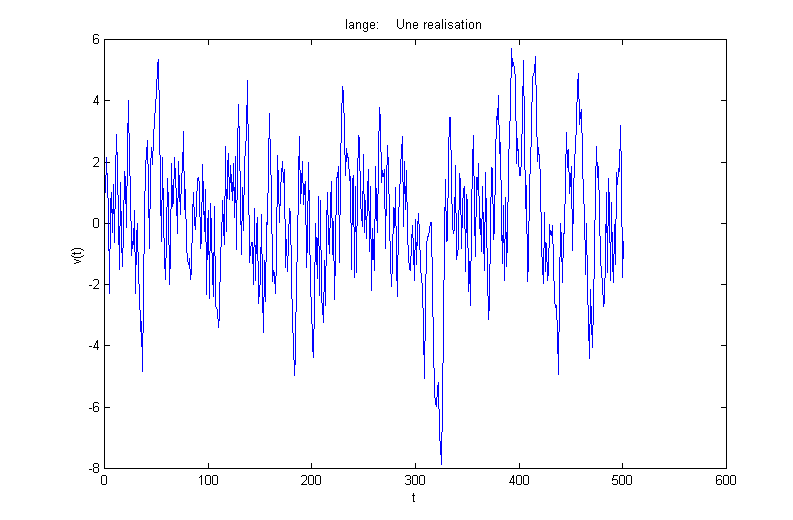

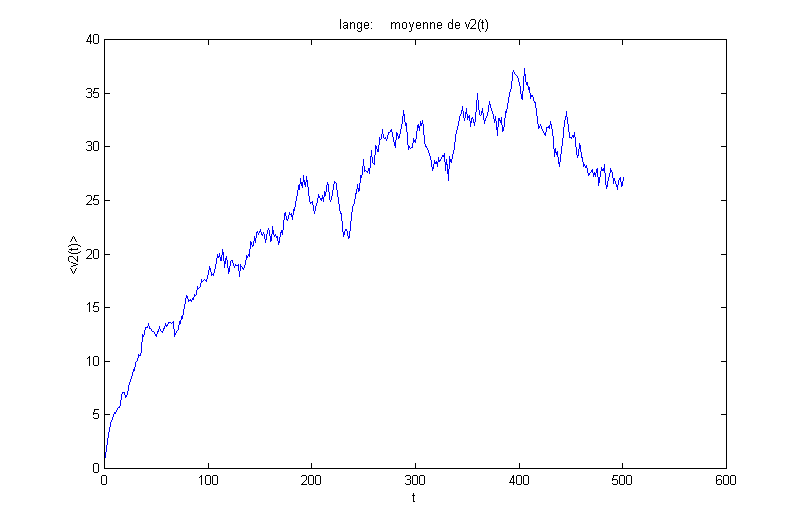
On remarque que la force de frottement faiblit quand v grandit. Aussi, il est normal de voir la moyenne de la vitesse au carré croître.